独立筹码模型(ICM)让我们清晰地理解在德州锦标赛中每个决策的奖励影响,它能指引我们的策略应该更紧还是更激进。然而,在牌桌上即时计算ICM是不可能的,但我们有一个替代方案:那就是泡沫系数。它能让我们在锦标赛的每个阶段做出更明智的决策。
一、什么是泡沫系数?
泡沫系数用于衡量德州锦标赛中的ICM压力。它的定义是:当你在锦标赛中输掉全压所损失的锦标赛权益$EV,与当你赢得全压时所获得的$EV之间的比率。实际上,泡沫系数显示了在锦标赛中你应该害怕谁,以及应该对谁采取激进行动。

泡沫系数由Lee Nelson、Steven L.Heston和Tysen Streib在他们2009年开创性的著作《Kill Everyone》中首次提出。尽管它在提出时并未立即被广泛接受和使用,但在solver时代它重新获得了关注。
由于名字的缘故,泡沫系数有时被误认为是一个只需要在锦标赛的泡沫阶段关注的指标。
这也是一些玩家对ICM的误解,认为它只适用于进入奖励圈之前。但其实ICM和泡沫系数会在锦标赛的每个阶段影响你的策略。
二、泡沫系数的例子
ICM的一个基本原则是,当我们参与一个底池时,我们赢得的权益永远不如我们可能失去的多。这是因为MTT的奖励结构决定了我们赢得的权益从来不及筹码的增长那么多。
让我们来看一个$100买入、10人SNG的简化游戏例子,筹码量为1000,奖励分配为$500/$300/$200。在这个例子中,没有服务费或前注,盲注为50/100。
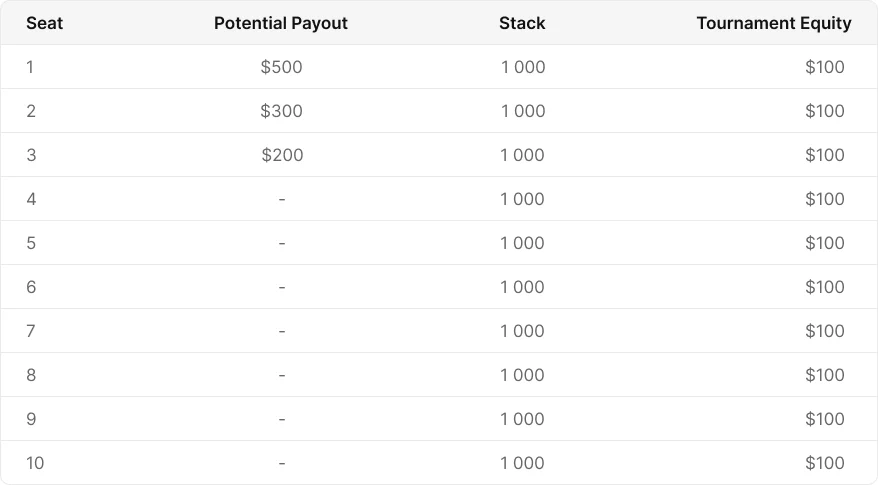
在没有发牌之前,每个人的权益都是$100,这与他们的买入金额一致。但假设小盲和大盲在第一手全压,小盲输了。这个时候权益会发生什么变化?
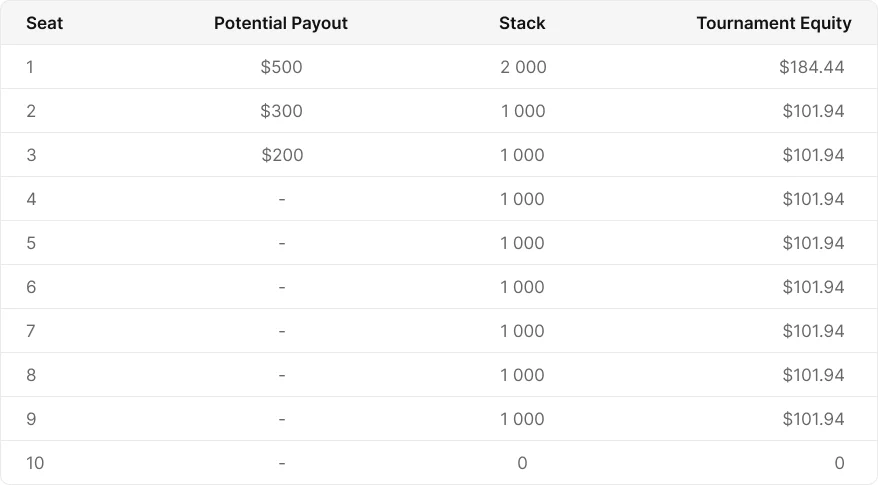
输掉的玩家的权益从$100降到了$0,因为他被淘汰了。然而,赢得的玩家并没有获得$100的权益,而是仅获得了$84.44的权益。剩下的$15.56重新分配给了其他人!其他所有人没有冒任何风险,但他们的权益增加了$1.94,因为他们离奖励圈更近了一步。
赢得的玩家冒了$100的风险,却只赢得了$84.44的权益,这表明在锦标赛中,损失比赢得的收益更高。如果这是常规桌游戏,他们将冒$100风险赢得$100(我们称之为ChipEV)。筹码的价值和它们所代表的金钱价值完全相等。
由于奖励结构的原因,在锦标赛中,你永远不可能赢得比你风险更多的权益(除非涉及赏金)。比如最终冠军也并不是赢得$1000(10 x$100),冠军只赢得了$500,剩下的$500分配给了第二名($300)和第三名($200)。
泡沫系数显示了你在基于实际奖励权益的情况下需要跟注全压的权益。
泡沫系数的计算公式如下:
你失去的$EV/你赢得的$EV=泡沫系数
你将你可能失去的奖励价值除以你可能获得的奖励价值,所以在上面的例子中,它是:
$100/$84.44=1.18
当你得到泡沫系数后,你可以通过这个简单的计算来获得跟注全压所需的权益:
所需权益=泡沫系数/(泡沫系数+1)
在这个例子中,它是:
1.18/(1.18+1)=54.1%
如果这是常规桌游戏,两个玩家大约需要50%的权益来实现盈亏平衡。然而,因为这是锦标赛,权益要求上升到了54.1%。这仅仅是在锦标赛的早期阶段,这表明ICM在你做的每一个决策中都起着重要作用,而不仅仅是在接近奖励圈时。
三、什么影响泡沫系数?
泡沫系数是ICM压力的衡量指标,因此以下因素会影响泡沫系数:
奖励结构
锦标赛的阶段
筹码量
1.奖励结构
奖励结构对泡沫系数有很大的影响。在极端情况下,比如赢家通吃的锦标赛,泡沫系数为1。这类锦标赛完全不受泡沫系数的影响,从头到尾都是ChipEV策略。
在另一极端是卫星赛,所有的奖励价值相等,你要么拿到最低奖励,要么就出局。因此,在这些锦标赛中,ICM压力极大,甚至在某些情况下,正确的策略是翻前弃掉AA。
PKO(赏金赛)也可以使用泡沫系数。在这些锦标赛中,由于赢得赏金所增加的额外权益,泡沫系数可以低于1。例如,下图显示了PKO锦标赛第一手牌时每个玩家的泡沫系数。
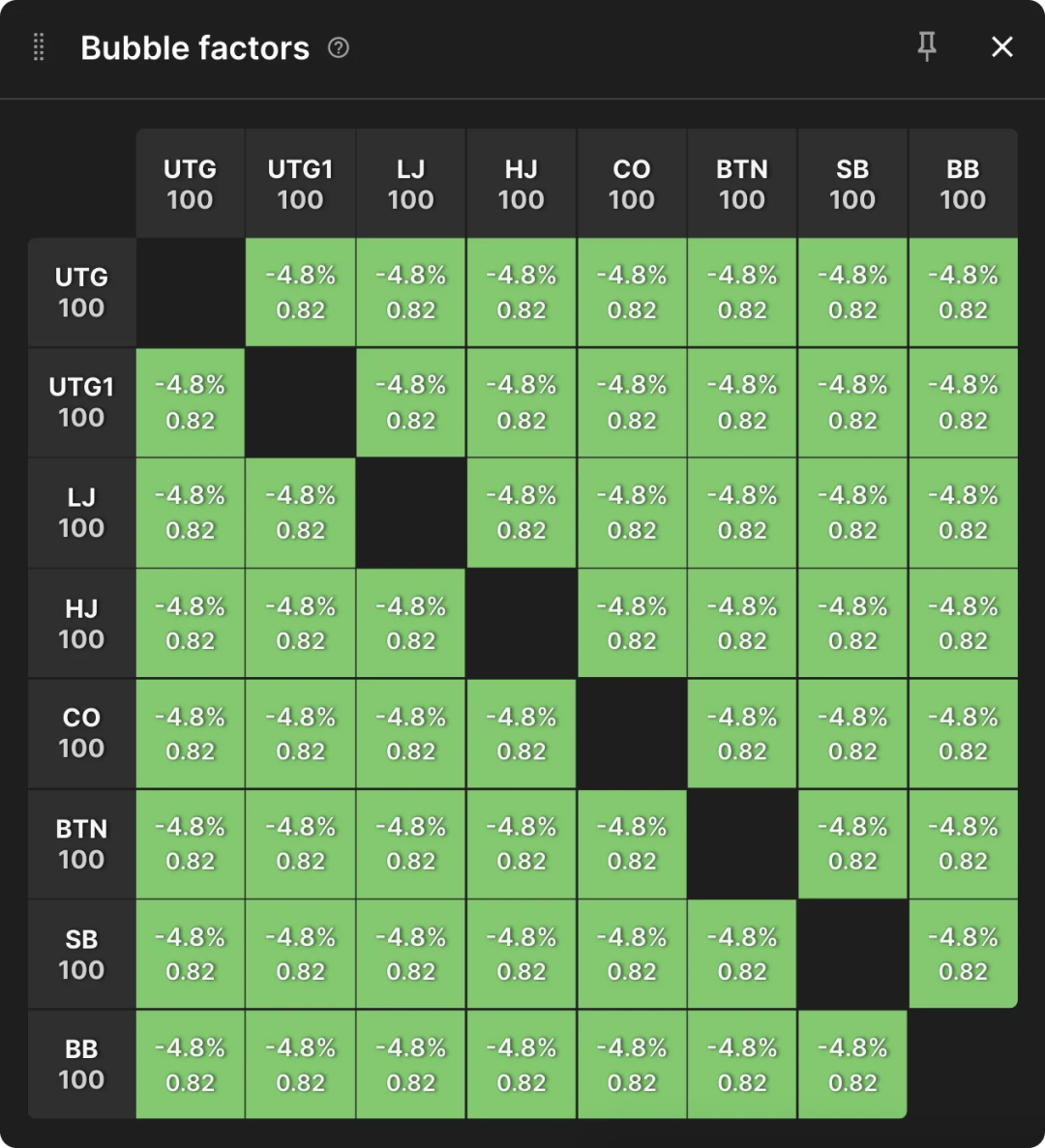
可以看到,所有玩家的泡沫系数都为0.82,这意味着每个玩家只需要45%的权益就可以跟注全压。这种负的风险溢价是由赏金导致的,对应的结果是玩家应该玩得比ChipEV范围更宽。PKO的第一手牌是唯一每个玩家都有机会打光其他玩家并赢得赏金的情况,这也是为什么PKO中跟注范围会非常宽的原因。
2.锦标赛阶段
你离奖励圈或决赛桌越近,ICM压力就越大。最好的例子来自于前面提到的《Kill Everyone》一书中的图表。
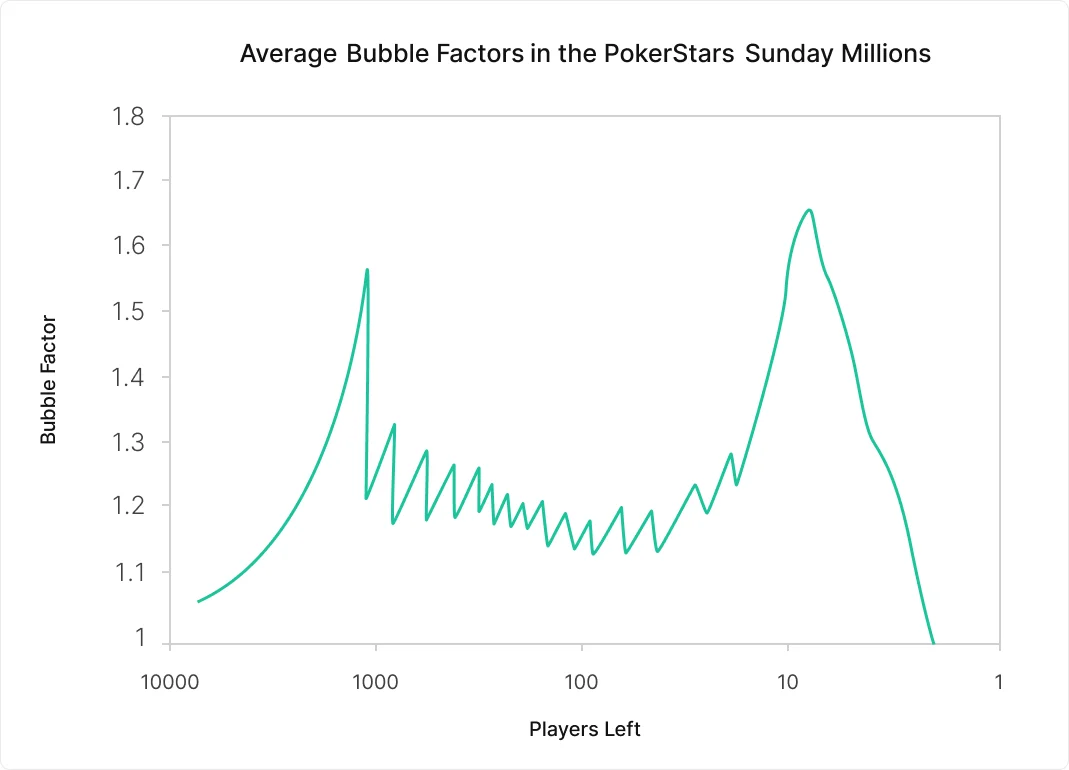
该图表显示了Sunday Million锦标赛中10,000名玩家的平均泡沫系数(基于2009年奖励结构)。
平均泡沫系数一开始较低,然后在奖励圈前急剧上升到1.6,一旦进入奖励圈,它会显著下降。图中还有一些小的波峰和波谷,代表的是奖励跳跃。接着,在决赛桌前又急剧上升到1.7,然后逐渐下降,直到单挑阶段。单挑阶段泡沫系数回归到1,即ChipEV,因为此时ICM不再适用。
决赛桌泡沫通常是ICM压力最大的阶段,因为决赛桌是争夺最大额奖励的地方。
3.筹码量
最后一个影响泡沫系数的因素,可能也是最重要的研究领域,是你所在桌上的筹码分布。我们之前讨论的是平均泡沫系数,但泡沫系数因你的筹码、位置和对手的筹码量而有很大不同。
大致来说:
筹码领先者(Chip leader,下用CL简称)的泡沫系数较低。这是直观的,因为他们被淘汰的风险最小,因此可以更自由地跟注全压。
短码也往往有较低的泡沫系数。他们的锦标赛权益本来就不多,所以与其他玩家交锋时冒的风险较小。
中等筹码的泡沫系数最高。对他们来说,在一堆短码之前被淘汰将是灾难性的,所以他们必须打得非常紧。
让我们看一个例子。这是一个筹码平均25bb的决赛桌局面:
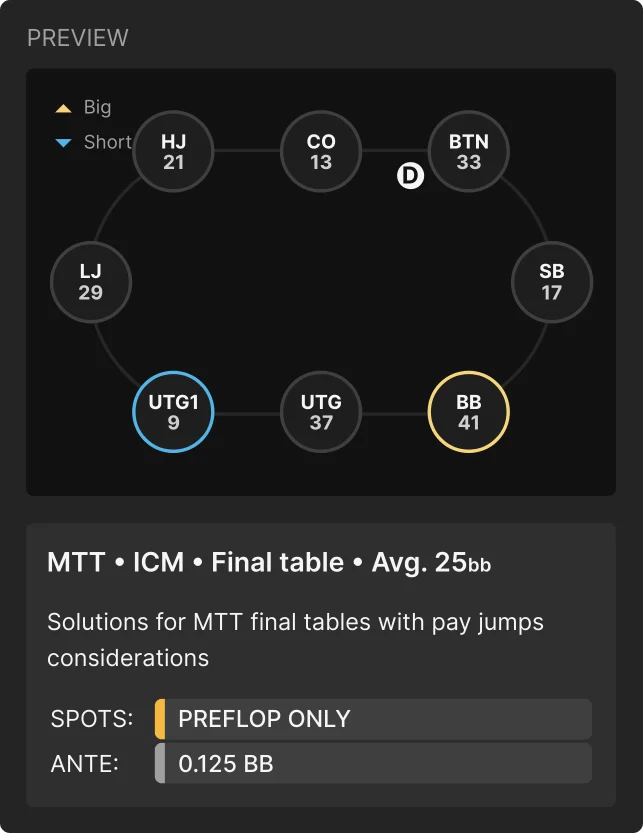
CL在BB位置有41bb,而UTG也有一个37bb的大码。中等码量在17到33bb之间,而两个短码都在14bb以下。
以下是桌上每个玩家互相对抗的泡沫系数:
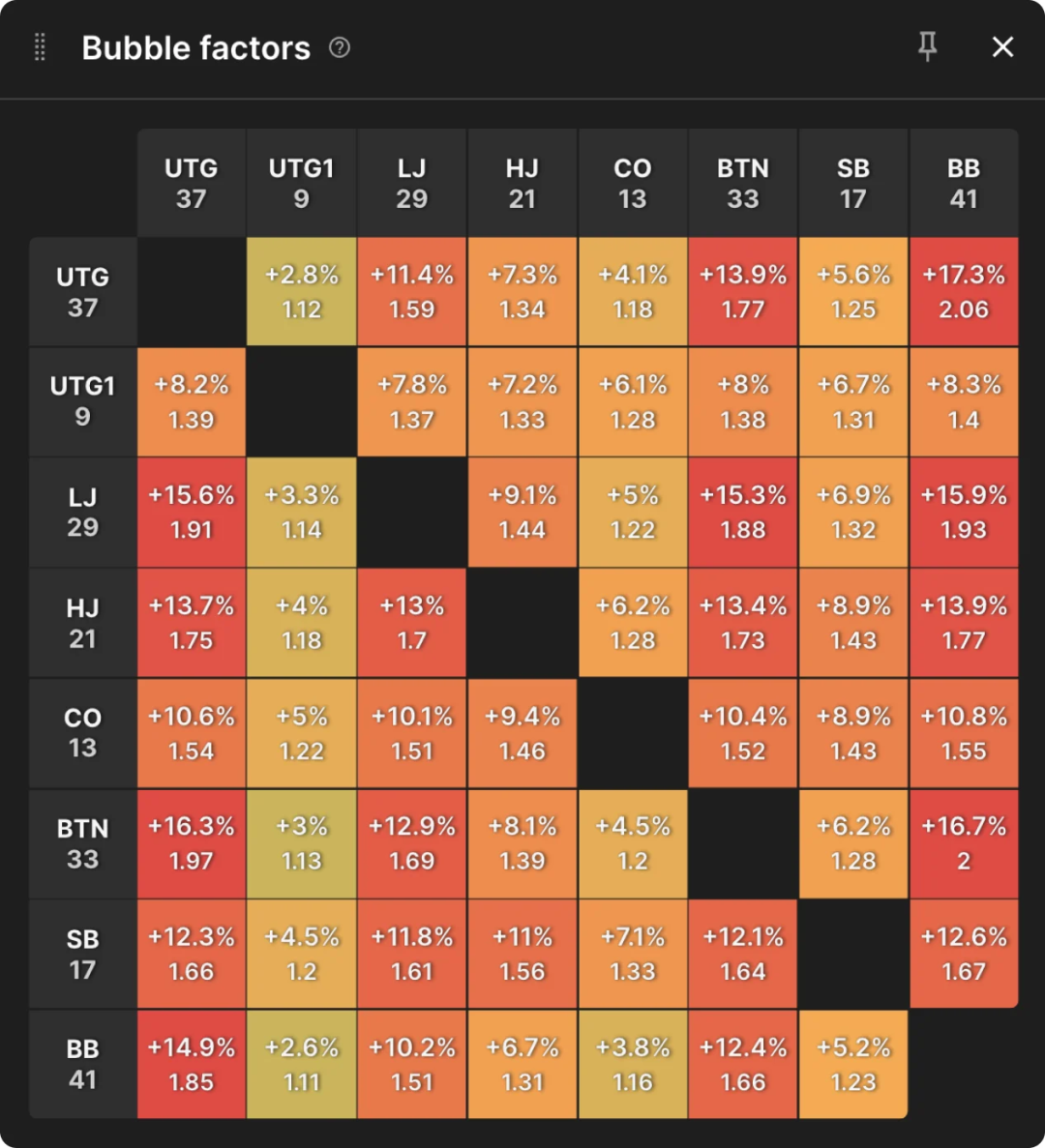
CL的泡沫系数最低可以低至1.11(面对最短码UTG1),接近ChipEV。UTG1作为最短码,泡沫系数也较低,最低为1.28。LJ拥有29bb,是中等码量之一,其泡沫系数非常高,对抗CL时高达1.93——对于这个玩家来说,被淘汰将是灾难性的,因为他很可能轻松地再往上爬四个名次。
除此以外我们还能看到,CL在面对UTG(第二长码)时泡沫系数为1.85,也相当高。而中码LJ在面对最短码时泡沫系数仅为1.14,等等。
泡沫系数是一个相对指标。你的筹码量决定了你的整体泡沫系数,但你的筹码量与对手筹码量之间的相对差异同样重要。
总结几个不同筹码量玩家的泡沫系数情况:
CL
CL在面对筹码第二的玩家时泡沫系数也很高。他不会被淘汰,但输给第二大码将对他来说几乎是同样的ICM灾难。然而,CL面对其他中等码量和短码时的风险溢价要低得多。
第二长码
UTG玩家以37bb的筹码量排名第二。如果CL已经弃牌,第二长码将成为实际上的CL。他可以安全地压制其他玩家,因为他知道自己不会被淘汰。但当他与CL争夺一个底池时,他自己被淘汰的风险非常大。因此,他的泡沫系数为2.06。他需要67%的权益才能跟注全压,而面对短码时他只需要53%的权益。
短码
最短码UTG1拥有9bb,其泡沫系数在1.28到1.4之间,取决于对手是谁。短码通常面临较低的风险溢价,因为他们本来就没有太多的锦标赛权益。各个泡沫系数之间的差异不大,因为无论输给谁,结果都是一样被淘汰。不过值得注意的是,最短码的泡沫系数在面对第二短码时最低,即面对13bb的CO时的泡沫系数为1.28。
这个差异很微小,但我们可以稍稍探讨下原因。赢得与第二短码的全压对决有更多的上行空间。如果CO输掉这手牌,他将成为一个微码,并非常接近被淘汰。而UTG1将拥有超过18bb的筹码,并且很可能至少能再爬一个名次。相比之下,面对CL实现筹码翻倍的收益并没有那么明显。
四、泡沫系数如何影响策略?
泡沫系数给我们的关键启示是,如何理解在桌上应该躲避谁以及应该对谁采取激进行动。
泡沫系数最准确的用途是计算跟注全压所需的权益。你也可以将其应用于翻后阶段,但计算会非常复杂。与其如此,不如将其作为衡量对手应该对你有多害怕,以及你应该对他们有多害怕的标准。这适用于你的翻前和翻后策略。
作为大码,最适合欺压的玩家是中码,他们对抗你风险极大,收益有限。你应该避免与其他大码对抗,需要有非常强的手牌才能与他们争夺底池。你还应该预料到短码会更积极地防守自己,因为他们很快就需要积极全压。
作为中码,你应该避免与大码和其他中码对抗,而可以稍微针对短码。或许最重要的是,你应该意识到自己处于“ICM棺材”中,此时没有任何选项是绝佳的。中码最重要的是采用“苟名次”的策略。
短码应该打得更松一些,同时可以针对其他短码。你可以对其他短码施加一些ICM压力,而赢得与他们全压对局的上行潜力更大。
五、总结
在牌桌上尝试计算泡沫系数并不是最好的学习方式。更简单且更有效的方法是在学习研究时深入理解什么是泡沫系数以及哪些因素会影响它。
关键要点:
比较不同筹码量的对局、锦标赛的不同阶段和不同的奖励结构。你很快就会发现在哪里施加ICM压力以及何时应该更保守。
在常规锦标赛中,你总是会失去比你获得的更多的锦标赛权益(即泡沫系数永远大于1)
泡沫系数告诉你跟注全压所需的权益
所需权益=泡沫系数/(泡沫系数+1)
奖励结构、锦标赛阶段和筹码量都会影响泡沫系数
在奖励圈和决赛桌之前阶段泡沫系数最高
泡沫系数在不同筹码量之间是不同的
大码应避免与大码对抗,欺压目标是中码
中码应避免与大码和其他中码对抗
短码应针对所有人,尤其是其他短码








